

Segundo sua página na Wikipédia, Octave é uma linguagem computacional desenvolvida para a computação matemática. Então podemos fazer uso desta linguagem para resolver problemas básicos ou complexos do mundo da matemática. Neste artigo vamos aprender juntos como calcular uma equação de segundo grau com Octave.
Uma equação de 2º Grau é normalmente representadas por Ax²+Bx+C=0 onde os coeficientes A, B e C são números reais. Ah, um detalhe importante, o coeficiente A deve ser sempre diferente de zero (A≠0). Mais adiante você entenderá o motivo. Ao resolvermos uma equação de segundo grau estamos empenhados em descobrir quais valores aplicados em x irão tornar o valor da expressão igual a zero. Estes valores são chamados de raízes.
Tenho certeza de que você já deve ter ouvido falar no método de Bhaskara* para descobrir as raízes de uma equação de 2ª Grau. Num futuro não tão distante, pretendo criar um post exclusivo para falarmos sobre este método, mas por hora, o que precisamos é nos orientar pela seguinte equação:
Figura 1: Fórmula de Bhaskara
O algoritmo de Bhaskara para resolver uma equação de segundo grau no Octave segue os seguintes passos:
Devemos solicitar ao usuário que digite os valores de a,b e c com os seguintes comandos:
a = input('Entre com a: ');
b = input('Entre com b: ');
c = input('Entre com c: ');
Realizamos o cálculo do delta com os dados informados pelo usuário:
delta = b^2 - 4*a*c;
Se o valor de Delta for maior que zero (Δ>0) teremos duas raízes reais e distintas.
if delta>0
disp('A equação tem duas raizes reais distintas');
x1 = (-b - sqrt (delta))/(2*a);
x2 = (-b + sqrt (delta))/(2*a);
disp(['O valor de x1 é: ',num2str(x1)]);
disp(['O valor de x2 é: ',num2str(x2)]);
Caso o valor de Delta seja igual a zero (Δ=0) teremos duas raízes reais e iguais.
elseif delta==0 disp(['A equação tem duas raizes reais iguais que são: ', num2str(-b/(2*a))]);
E por fim, caso o valor de Delta seja inferior a zero (Δ<0) teremos duas raízes iguais porém complexas (raíz de número negativo).
else
disp('A equação tem duas raizes complexas');
A seguir é exibido o código completo para o cálculo de equação de segundo grau utilizando Bhaskara e Octave.
a = input('Entre com a: ');
b = input('Entre com b: ');
c = input('Entre com c: ');
delta = b^2 - 4*a*c;
if delta>0
disp('A equação tem duas raizes reais distintas');
x1 = (-b - sqrt (delta))/(2*a);
x2 = (-b + sqrt (delta))/(2*a);
disp(['O valor de x1 é: ',num2str(x1)]);
disp(['O valor de x2 é: ',num2str(x2)]);
elseif delta==0
disp(['A equação tem duas raizes reais iguais que são: ', num2str(-b/(2*a))]);
else
disp('A equação tem duas raizes complexas');
end
A execução do script para calcular alguns valores de uma equação de segundo grau no Octave utilizando o método de Bhaskara é exibido na Figura 2:
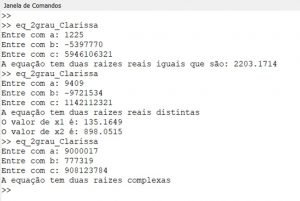
Figura 2: Resultado da Execução do Algoritmo para alguns valores.
Você alguma vez já tentou realizar uma divisão por zero na calculadora? Se ainda não tentou, vá em frente, faça o teste. Se o fizer num celular, provavelmente você receberá uma mensagem escrita informando que Não é possível dividir por 0. Dividir um número por zero é o mesmo que perguntar “qual número vezes zero dá outro número?” Obviamente não existe nenhum número que multiplicado por zero vá dar outro número, portanto dizemos que esta é uma divisão indefinida, já que não podemos definir um valor em uma divisão com o zero sendo o denominador.
É por este motivo que não podemos ter a variável A com o valor zero, já que isto resultaria numa divisão por zero, gerando uma indefinição.
E aí, ficou com alguma dúvida sobre Equação de Segundo Grau ou o funcionamento do script no Octave? Deixe sua dúvida aqui nos comentários ou entre em contato comigo que terei o maior prazer em lhe ajudar 😀.
Aproveite e ganhe um desconto exclusivo de 50% na sua primeira aula particular. Tire aquela dúvida que você sempre teve ou monte um plano de estudos personalizado e otimize os seus resultados.